Global Gauss-Bonnet theorem
It is the global version of local Gauss-Bonnet theorem.
Theorem
Given a closed orientable surface (I think it should be immersed in $\mathbb{R}^3$) $S$ of genus $g$, the total curvature
$$ K_S=\int_S K(p) dA $$where $K$ is the Gaussian curvature, satisfies
$$ K_S=4\pi(1-g)=2 \pi (2-2g). $$The quantity
$$ \mathcal{X}(S)=2-2g $$is the Euler characteristic.
$\blacksquare$
It means that given any closed orientable surface, if we deform it in the way we like (even stretching and twisting), if we get an increase in Gaussian curvature in a point, the curvature must be decreasing in other points in order to compensate the total curvature.
Visual idea:
(@needham2021visual pages 169-172)
In a sphere, or in any other topologically equivalent surface, the total curvature is $4\pi$, since the unitary normal vector fill $\mathbb{S}^2$ exactly once.
In a torus is 0, since the external side of the torus counts for $4\pi$ but the internal one add $-4\pi$, since the Gauss map reverse orientation in these points.
In the general case of a compact surface:
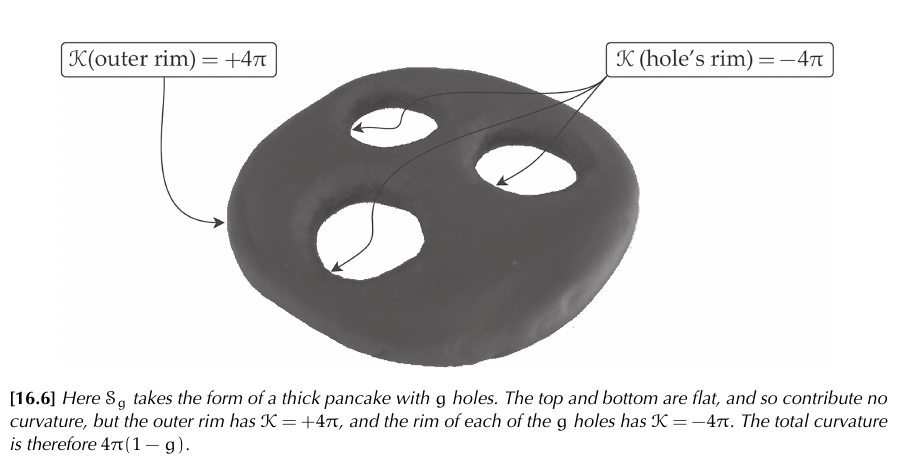
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: